LIMIT FUNGSI
Assalamualaikum Warahmatullahi Wabarakatuh.
Haloo
semuanya, selamat datang di blog aku, kali ini aku akan membagikan
sedikit materi kalkulus 1 tentang limit fingsi. Semoga tulisan ini
bermanfaat dan dan dapat membantu kalian dalam belajar. Selamat membaca.
KALKULUS 1 : LIMIT FUNGSI
Toerema / Pernyataan:
)
)
^{2}-2(-1)+1}{(-1)+2}=\frac{1+2+1}{-1+2}=\&space;4)

Setelah disubstitusikan ternyata nilai limit tersebut tidak terdefinisi atau merupakan bentuk tak tentu .
Maka dari itu untuk menentukan nilai suatu limit harus menggunakan
metode lain. Apabila diperhatikan, pada f(x) terdapat bentuk akar yaitu
.
Maka dari itu untuk menentukan nilai suatu limit harus menggunakan
metode lain. Apabila diperhatikan, pada f(x) terdapat bentuk akar yaitu sehingga metode perkalian dengan akar sekawaran dapat dilakukan pada kasus seperti ini.
sehingga metode perkalian dengan akar sekawaran dapat dilakukan pada kasus seperti ini.
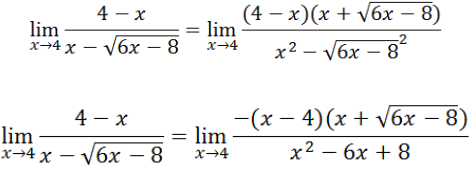
Bentuk dapat difaktorkan menjadi
dapat difaktorkan menjadi 

Jadi, nilai limit fungsi aljabar tersebut adalah -4
SUMBER: https://galeryofkalkulus.blogspot.com/2019/04/limit-fungsi.html
KALKULUS 1 : LIMIT FUNGSI
A. Konsep Limit Fungsi Aljabar
Limit
dapat diartikan sebagai menuju suatu batas, sesuatu yang dekat namun
tidak dapat dicapai. Dalam bahasa matematika, keadaan ini dapat disebut
limit. Mengapa harus ada limit? limit menjelaskan suatu fungsi jika
batas tertentu didekati. Mengapa harus didekati? karena suatu fungsi
biasanya tidak terdefinisi pada titik-titik tertentu. Walaupun suatu
fungsi seringkali tidak terdefinisi untuk titik tertentu, namun masih
dapat dicari tahu berapa nilai yang didekati oleh fungsi tersebut
apabila titik tertentu semakin didekati yaitu dengan limit.
Maksudnya, apabila x mendekati a namun x tidak sama dengan a maka f(x) mendekati L. Pendekatan x ke a dapat dilihat dari dua sisi yaitu sisi kiri dan sisi kanan atau dengan kata lain x dapat mendekati dari arah kiri dan arah kanan sehingga menghasilkan limit kiri dan limit kanan.
Untuk nilai x yang mendekati 1
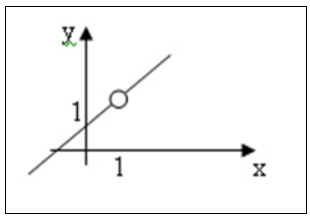
Berikut gambar grafiknya:
Berdasarkan gambar grafik diatas dapat dijelaskan:
- Apabila x mendekati 1 dari kiri, maka nilai f(x) mendekati 2
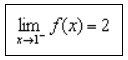
- Apabila x mendekati 1 dari kanan, maka nilai f(x) mendekati 2

- Jadi, apabila x mendekati 1, maka nilai f(x) mendekati 2
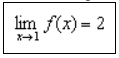
Toerema / Pernyataan:
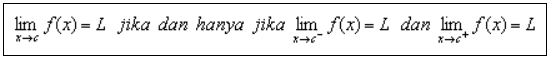
Suatu fungsi dikatakan mempunyai limit apabila antara limit kiri dan limit kannya mempunyai besar nilai yang sama dan apabila limit kiri dan limit kanan tidak sama maka nilai limitnya tidak ada.
B. Sifat-sifat Limit Fungsi Aljabar
Apabila n merupakan bilangan bulat positif, k konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifat di bawah ini berlaku. 

C. Menentukan Nilai Limit Fungsi Aljabar
Ada 2 bentuk dalam menentukan limit fungsi aljabar yaitu:
Bentuk pertama
Bentuk kedua
Dalam
hubungannya dengan bentuk limit yang pertama ada beberapa metode dalam
menentukan nilai limit fungsi aljabar yaitu dengan cara substitusi dan
cara pemfaktoran.
1. Cara Substitusi
Cara
substitusi ini langkahnya dengan mengganti peubah yang mendekati nilai
tertentu dengan fungsi aljabarnya. Berikut adalah beberapa contoh yang
dapat dipahami.
Contoh 1:
Tentukan nilai limit fungsi aljabar dari
-1=3-1=2)
Jadi, nilai dari limit fungsi aljabar tersebut, 

Contoh 2:
Tentukan nilai limit fungsi aljabar dari


Jadi, nilai dari limit fungsi aljabar tersebut, 

Contoh soal 3:
Tentukan nilai limit fungsi aljabar dari


Jadi, nilai dari limit fungsi aljabar tersebut, 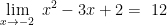
Contoh soal 4:
Tentukan nilai limit fungsi aljabar dari


Jadi, nilai dari limit fungsi aljabar tersebut, 

Contoh soal 5:
Tentukan nilai limit fungsi aljabar dari,


Jadi, nilai dari limit fungsi aljabar tersebut, 

Contoh 6:
Tentukan nilai limit fungsi aljabar dari
^{3}}{(0)^{2}-1}=\&space;\frac{0}{-1}=\&space;0)
Jadi, nilai dari limit fungsi aljabar tersebut, 

Contoh 7:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut, 

2. Cara Pemfaktoran
Cara
pemfaktoran digunakan apabila cara substitusi menghasilkan nilai limit
yang tidak terdefinisikan seperti pada contoh berikut: ^{2}-4}{2-2}=\&space;\frac{4-4}{2-2}=\&space;\frac{0}{0})
Cara
pemfaktoran dilakukan dengan langkah menentukan faktor persekutuan
antara pembilang dan penyebuntya. Berikut beberapa contoh untuk
dipahami.
Contoh 1:
Tentukan nilai limit fungsi aljabar dari
}}{(x+2)}}{{\color{Red}&space;(x-2)}}=\lim_{x\rightarrow&space;2}\&space;(x+2)=\&space;(2)+2=\&space;4)
Jadi, nilai dari limit fungsi aljabar tersebut, 

Contoh 2:
Tentukan nilai limit fungsi aljabar dari
}(x+5)}{{\color{Red}&space;(x-1)}}=\lim_{x\rightarrow&space;1}(x+5)=(1)+5=6)
Jadi, nilai dari limit fungsi aljabar tersebut, 

Contoh 3:
Tentukan nilai limit fungsi aljabar dari

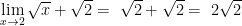

Jadi, nilai dari limit fungsi aljabar tersebut, 

Contoh soal 4:
Tentukan nilai limit fungsi aljabar dari }(5x-1)}{{\color{Red}&space;(x+2)}})
=\textup{&space;}{5(-2)-1}=-10-2=&space;-11)
Jadi, nilai dari limit fungsi aljabar tersebut, 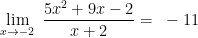
Contoh soal 5:
Tentukan nilai limit fungsi aljabar dari
=\lim_{x\rightarrow&space;3}\textup{&space;}\frac{{\color{Red}&space;x}(x-3)}{{\color{Red}&space;x}(x^{2}+2x-15)})
}{(x^{2}+2x-15)}=\lim_{x\rightarrow&space;3}\frac{{\color{Red}&space;(x-3)}}{{\color{Red}&space;(x-3)}(x+5)})
}=\textup{&space;}&space;\frac{1}{(3)+5}=\textup{&space;}\frac{1}{8})
Jadi, nilai dari limit fungsi aljabar tersebut, =\textup{&space;}\frac{1}{8})
Dalam
hubungannya dengan bentuk limit yang kedua ada beberapa cara dalam
menentukan nilai limit fungsi aljabar yaitu metode membagi dengan
pangkat tertinggi penyebut dan metode mengalikan dengan faktor sekawan.
1. Metode membagi dengan pangkat tertinggi penyebut
contoh 1:
Tentukan nilai limit fungsi aljabar dari
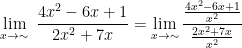
Besar pangkat pembilang dan penyebut dalam soal ini adalah 2, maka 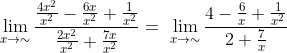
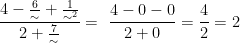
Jadi, nilai dari limit fungsi aljabar tersebut, 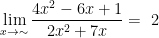
Contoh 2:
Tentukan nilai limit fungsi aljabar dari
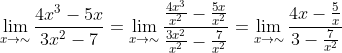
Besar pangkat pembilang dan penyebut dalam soal ini adalah 3, maka -\frac{5}{(\sim&space;)}}{3-\frac{7}{(\sim&space;)^{2}}}=\frac{\sim&space;-0}{3-0}=\frac{\sim&space;}{3}=\sim)
Jadi, nilai dari limit fungsi aljabar tersebut, 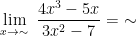
Contoh soal 3:
Tentukan nilai limit fungsi aljabar dari
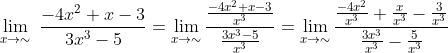
Besar pangkat pembilang dan penyebut dalam soal ini adalah 3, maka 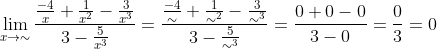
Jadi, nilai dari limit fungsi aljabar tersebut, 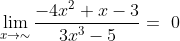
2. Metode mengalikan dengan faktor sekawan
Contoh soal:
Tentukan nilai limit dari 
Langkah
awal yang perlu dilakukan untuk menentukan nilai suatu limit yaitu
dengan mensubtitusikan x=c ke f(x), sehingga dalam kasus ini
substitusikan
x=4 ke
x=4 ke

Setelah disubstitusikan ternyata nilai limit tersebut tidak terdefinisi atau merupakan bentuk tak tentu
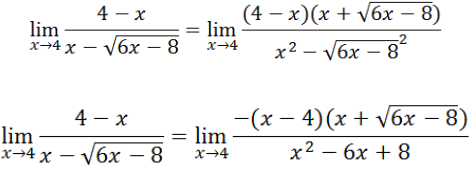
Bentuk

Jadi, nilai limit fungsi aljabar tersebut adalah -4
SUMBER: https://galeryofkalkulus.blogspot.com/2019/04/limit-fungsi.html
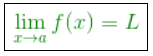




Komentar
Posting Komentar