Label

KALKULUS 2 : INTEGRAL PARSIAL

Integral Parsial

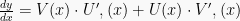
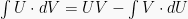
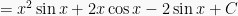
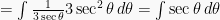
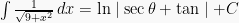
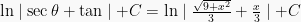
 Assalamualaikum Warahmatullahi Wabarakatuh
Selamat datang di blog saya, kali ini saya akan membagikan sedikit materi tentang integral parsial, selamat membaca dan semuga bermanfaat. :)

Dalam pengintegralan, selain operasi biasa atau dengan teknik substitusi, ada teknik lain yaitu integral parsial. Teknik ini digunakan jika pada teknik sebelumnya tidak bisa digunakan. Teknik ini merupakan integral dari turunan hasil kali dua fungsi. Berikut ini adalah konsep integral parsial:
Jika y = U(x) . V(x), maka:
\frac{dy}{dx}=V(x) \cdot U',(x)+U(x) \cdot V',(x)
dy = v(x) \cdot U' (x)dx+U(x) \cdot V' (x)\, dx
Jika y diganti UV maka:
d(UV) = V(x) \cdot U' (x)\, dx+U(x) \cdot V'(x)\, dx
Karena diketahui bahwa U' (x) dx = dU dan V' (x) dx = dV, maka persamaan menjadi:
d(UV) = V . dU + U . dV
U . dV = d(UV) – V . dU
Dengan mengintegralkan kedua ruas dalam persamaan diatas, diperoleh:
Rumus ntegral parsial:
\int U \cdot dV = UV -\int V \cdot dU
Perlu diperhatikan untuk memilih U dan dV yang tepat agar pengintegralan memberikan hasil. (dV) harus dipilih yang dapat diintegralkan dengan rumus, sedangkan yang lain menjadi U.
Contoh Soal Integral Substitusi dan Parsial dan Pembahasan
Contoh Soal 1Contoh Soal 2
Dalam integral parsial, terkadang bisa menurunkan U dan mengintegralkan dV secara berulang. Jika terjadi proses yang berulang, maka proses dapat diringkas. Sebagai contoh \int x^2 \cos x\, dx adalah:
integral parsial
Maka diperoleh hasil:
\int x^2 \cos x\, dx = (x^2 \cdot \sin x)-(2x \cdot - \cos x)+(2 \cdot - \sin x)+C
=x^2 \sin x+2x \cos x - 2 \sin x + C
Tentukanlah hasil dari \int \cos^2 2x \sin 2x\, dx.
Pembahasan 1:
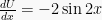Misalkan U = \cos 2x dan \frac{dU}{dx}=-2 \sin 2x, maka
dU = -2 sin 2x dx
-\frac{dU}{2}= \sin 2x\, dx
Sehingga,
\int \cos^2 2x \sin 2xdx=\int U^2 (-\frac{1}{2})dU =(-\frac{1}{2})(\frac{u^3}{3})=-\frac{u^3}{6}
Kemudian 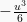-\frac{u^3}{6} disubstitusi dengan nilai U menjadi :
-\frac{U^3}{6} = -\frac{\cos^3 2x}{6}
Tentukan hasil dari 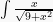 \int\frac{x}{\sqrt{9+x^2}}
Pembahasan 2:
Misalkan trigonometrinya adalah:
integral substitusi trigonometri
Nilai x = 3 \tan \theta dan dx = 3 \sec^2 \theta\, d \theta dan x^2 = 9 \sec^2 \theta.
Sehingga:
\int\frac{1}{\sqrt{9+x^2}}\, dx = \int\frac{1}{\sqrt{9+9 \sec^2\theta}}3 \sec^2\theta\, d\theta
=\int\frac{1}{3 \sec\theta}3 \sec^2\theta\, d\theta =\int \sec\theta\, d\theta
\int\frac{1}{\sqrt{9+x^2}}\, dx = \ln\mid \sec\theta + \tan\mid+C
Dengan segitiga diatas, nilai sec dan tan bisa diketahui. Sehingga:
\ln\mid \sec\theta + \tan\mid+C= \ln\mid \frac{\sqrt{9+x^2}}{3}+\frac{x}{3}\mid+C
= \ln\mid\frac{x+\sqrt{9+x^2}}{3}\mid+C= \ln\mid x+\sqrt{9+x^2}\mid- \ln\mid 3\mid+C

Oke teman teman, mungkin itu saja materi kali ini. Terimakasih sudah membaca. :)

Label:

Komentar

Posting Komentar

Postingan Populer