KALKULUS 2 : INTEGRAL SUBSTITUSI
Assalamualaikum warahmatullahi Wabarakatuh
Hallo Semuanya....
Selamat datang di blog saya, bagi kalian yang baru mampir, perkenalkan nama saya Ayu Rizkyca Awalia, mahasiswa semester 3 Sekolah Tinggi Teknik PLN Jakarta.
Seperti judulnya, kali ini saya akan membagikan sedikit materi tentang integral substitusi, sebenarnya materi ini harus dibahas sebelum materi integral substitusi trigonometri, tapi karena saya lupa, jadi baru sekarang saya bagikan. Sebelum terlalu banyak berbicara, kita langsung ke materinya saja...
Selamat membaca :)
 |
| RUMUS INTEGRAL SUBSTITUSI |
Ada yang tahu apa itu integral substitusi? Jadi......
atau ialah salah satu metode untuk mencari suatu integral dengan mensubstitusi salah satu variabel dan mengubahnya menjadi sebuah bentuk yang lebih sederhana. Ciri – ciri dari soal integral yang bisa diselesaikan dengan menggunakan rumus integral substitusi yaitu yang mempunyai faktor yang merupakan turunan dari faktor lainnya.


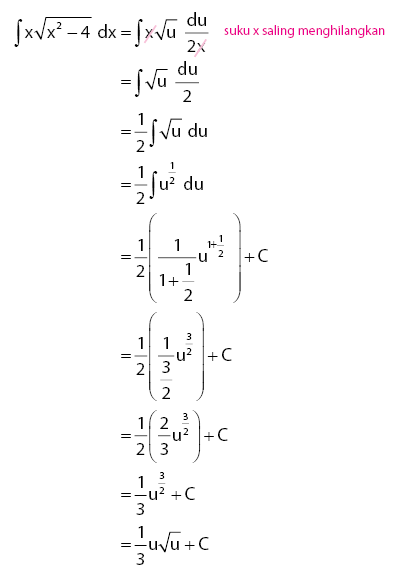
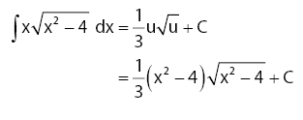


Komentar
Posting Komentar